Inequality of arithmetic and geometric means
In mathematics, the inequality of arithmetic and geometric means, or more briefly the AM–GM inequality, states that the arithmetic mean of a list of non-negative real numbers is greater than or equal to the geometric mean of the same list; and further, that the two means are equal if and only if every number in the list is the same.
Contents |
Background
The arithmetic mean, or less precisely the average, of a list of n numbers x1, x2, . . ., xn is the sum of the numbers divided by n:
The geometric mean is similar, except that it is only defined for a list of nonnegative real numbers, and uses multiplication and a root in place of addition and division:
If x1, x2, . . ., xn > 0, this is equal to the exponential of the arithmetic mean of the natural logarithms of the numbers:
The inequality
Restating the inequality using mathematical notation, we have that for any list of n nonnegative real numbers x1, x2, . . ., xn,
and that equality holds if and only if x1 = x2 = . . . = xn.
Geometric interpretation
In two dimensions, 2x1 + 2x2 is the perimeter of a rectangle with sides of length x1 and x2. Similarly, 4√(x1x2) is the perimeter of a square with the same area. Thus for n = 2 the AM-GM inequality states that a square has the smallest perimeter among all rectangles with equal area.
The full inequality is an extension of this idea to n dimensions. Every vertex on an n-dimensional box is connected to n edges. If these edges are given lengths x1, x2, ..., xn, then x1 + x2 + … + xn is the total length of edges connected to the vertex. There are 2n vertices, so multiply this by 2n; however, since each edge meets two vertices, that counts every edge twice. Thus we divide by 2 and conclude that there are n2n−1 edges. There are equally many edges of each length and n lengths; hence there are 2n−1 edges of each length. The total edge-length is therefore 2n−1(x1 + x2 + … + xn). On the other hand, ![2^{n-1} n \sqrt[n]{x_1 x_2 \cdots x_n}](/2012-wikipedia_en_all_nopic_01_2012/I/26168f5611edcc091b6c351e3173001b.png) is the total length of edges connected to a vertex on an n-dimensional cube of equal volume. Since the inequality says
is the total length of edges connected to a vertex on an n-dimensional cube of equal volume. Since the inequality says
we get
Thus the AM–GM inequality states that an n-cube has the smallest sum of lengths of edges connected to each vertex among all n-dimensional boxes with the same volume. [1]
Generalizations
- There is a similar inequality for the weighted arithmetic mean and weighted geometric mean. Specifically, let the nonnegative numbers x1, x2, . . ., xn and the nonnegative weights α1, α2, . . ., αn be given. Set
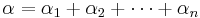 . If α > 0, then the inequality
. If α > 0, then the inequality
- holds with equality if and only if all the xk with αk > 0 are equal. Here the convention 00 = 1 is used.
- If all αk = 1, this reduces to the above AM–GM inequality.
Other generalizations of the inequality of arithmetic and geometric means include these:
Example application
Consider the following function:
for x, y, and z all positive real numbers. Suppose we wish to find the minimum value of this function. Rewriting a bit, and applying the AM–GM inequality, we have:
Further, we know that the two sides are equal exactly when all the terms of the mean are equal:
Proofs
Proof by induction
There are several ways to prove the AM–GM inequality; for example, it can be inferred from Jensen's inequality, using the concave function ln(x). It can also be proven using the rearrangement inequality. Considering length and required prerequisites, the proof by induction given below is probably the best recommendation for first reading.
With the arithmetic mean
of the non-negative real numbers x1,...,xn, the AM–GM statement is equivalent to
with equality if and only if μ = xi for all i = 1,...,n.
For the following proof we apply mathematical induction and only well-known rules of arithmetic.
Induction basis: For n = 1 the statement is true with equality.
Induction hypothesis: Suppose that the AM–GM statement holds for all choices of n non-negative real numbers.
Induction step: Consider n + 1 non-negative real numbers. Their arithmetic mean μ satisfies
If all numbers are equal to μ, then we have equality in the AM–GM statement and we are done. Otherwise we may find one number that is greater than μ and one that is smaller than μ, say xn > μ and xn+1 < μ. Then
Now consider the n numbers
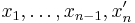 with
with 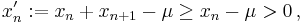
which are also non-negative. Since
μ is also the arithmetic mean of 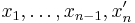 and the induction hypothesis implies
and the induction hypothesis implies
Due to (*) we know that
hence
in particular μ > 0. Therefore, if at least one of the numbers x1,...,xn−1 is zero, then we already have strict inequality in (**). Otherwise the right-hand side of (**) is positive and strict inequality is obtained by using the estimate (***) to get a lower bound of the right-hand side of (**). Thus, in both cases we get
which completes the proof.
Proof by Pólya
George Pólya provided a proof similar to what follows. Let f(x) = ex−1 − x, with derivative f'(x) = ex−1 − 1. Observe f'(1) = 0 and hence that f has an absolute minimum of f(1) = 0. Now x ≤ ex−1 for all real x.
Consider a list of non-negative numbers 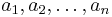 with arithmetic mean μ. By repeated application of the above inequality, we obtain the following:
with arithmetic mean μ. By repeated application of the above inequality, we obtain the following:
But the exponential argument can be simplified:
Returning to (1),
which produces the result: [2]
Proof by Cauchy
The following proof by cases relies directly on well-known rules of arithmetic but employs the rarely used technique of forward-backward-induction. It is essentially from Augustin Louis Cauchy and can be found in his Cours d'analyse.
The case where all the terms are equal
If all the terms are equal:
then their sum is nx1, so their arithmetic mean is x1; and their product is x1n, so their geometric mean is x1; therefore, the arithmetic mean and geometric mean are equal, as desired.
The case where not all the terms are equal
It remains to show that if not all the terms are equal, then the arithmetic mean is greater than the geometric mean. Clearly, this is only possible when n > 1.
This case is significantly more complex, and we divide it into subcases.
The subcase where n = 2
If n = 2, then we have two terms, x1 and x2, and since (by our assumption) not all terms are equal, we have:
as desired.
The subcase where n = 2k
Consider the case where n = 2k, where k is a positive integer. We proceed by mathematical induction.
In the base case, k = 1, so n = 2. We have already shown that the inequality holds where n = 2, so we are done.
Now, suppose that for a given k > 1, we have already shown that the inequality holds for n = 2k−1, and we wish to show that it holds for n = 2k. To do so, we proceed as follows:
where in the first inequality, the two sides are equal only if both of the following are true:
(in which case the first arithmetic mean and first geometric mean are both equal to x1, and similarly with the second arithmetic mean and second geometric mean); and in the second inequality, the two sides are only equal if the two geometric means are equal. Since not all 2k numbers are equal, it is not possible for both inequalities to be equalities, so we know that:
as desired.
The subcase where n < 2k
If n is not a natural power of 2, then it is certainly less than some natural power of 2, since the sequence 2, 4, 8, . . ., 2k, . . . is unbounded above. Therefore, without loss of generality, let m be some natural power of 2 that is greater than n.
So, if we have n terms, then let us denote their arithmetic mean by α, and expand our list of terms thus:
We then have:
so
as desired.
Proof of the generalized AM–GM inequality using Jensen's inequality
Using the finite form of Jensen's inequality for the natural logarithm, we can prove the inequality between the weighted arithmetic mean and the weighted geometric mean stated above.
Since an xk with weight αk = 0 has no influence on the inequality, we may assume in the following that all weights are positive. If all xk are equal, then equality holds. Therefore, it remains to prove strict inequality if they are not all equal, which we will assume in the following, too. If at least one xk is zero (but not all), then the weighted geometric mean is zero, while the weighted arithmetic mean is positive, hence strict inequality holds. Therefore, we may assume also that all xk are positive.
Since the natural logarithm is strictly concave, the finite form of Jensen's inequality and the functional equations of the natural logarithm imply
Since the natural logarithm is strictly increasing,
See also
References
- ^ Steele, J. Michael (2004). The Cauchy-Schwarz Master Class: An Introduction to the Art of Mathematical Inequalities. MAA Problem Books Series. Cambridge University Press. ISBN 978-0521546775. OCLC 54079548.
- ^ Arnold, Denise; Arnold, Graham (1993). Four unit mathematics. Hodder Arnold H&S. p. 242. ISBN 978-0340543351. OCLC 38328013.
- Augustin-Louis Cauchy, Cours d'analyse de l'École Royale Polytechnique, première partie, Analyse algébrique, Paris, 1821. The proof of the inequality of arithmetic and geometric means can be found on pages 457ff.
- Arthur Lohwater (1982). "Introduction to Inequalities". Online e-book in PDF format. http://www.mediafire.com/?1mw1tkgozzu.
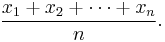
![\sqrt[n]{x_1 \cdot x_2 \cdots x_n}.](/2012-wikipedia_en_all_nopic_01_2012/I/d697f2a744c22e325772f817a6888f88.png)
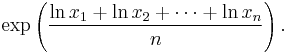
![\frac{x_1 %2B x_2 %2B \cdots %2B x_n}{n} \geq \sqrt[n]{x_1 \cdot x_2 \cdots x_n},](/2012-wikipedia_en_all_nopic_01_2012/I/ad81bec045dad351d43ab3ed0606434e.png)
![\sqrt[n]{x_1\cdots x_n} \le {x_1 %2B \cdots %2B x_n \over n},](/2012-wikipedia_en_all_nopic_01_2012/I/504d2c32a98a197cc435ee83fc4e384a.png)
![n2^{n-1} \sqrt[n]{x_1\cdots x_n} \le 2^{n-1}(x_1 %2B \cdots %2B x_n). \,](/2012-wikipedia_en_all_nopic_01_2012/I/44e3cc8d35498dc2816bc6fdf2cab4b4.png)
![\frac{\alpha_1 x_1 %2B \alpha_2 x_2 %2B \cdots %2B \alpha_n x_n}{\alpha} \geq \sqrt[\alpha]{x_1^{\alpha_1} x_2^{\alpha_2} \cdots x_n^{\alpha_n}}](/2012-wikipedia_en_all_nopic_01_2012/I/d7285ff8e6f3ba98e1dc0934631c1c20.png)
![f(x,y,z) = \frac{x}{y} %2B \sqrt{\frac{y}{z}} %2B \sqrt[3]{\frac{z}{x}}](/2012-wikipedia_en_all_nopic_01_2012/I/7f847e368bbc9196ce8f8ea6486e954a.png)

![= 6 \cdot \frac{ \frac{x}{y} %2B \frac{1}{2} \sqrt{\frac{y}{z}} %2B \frac{1}{2} \sqrt{\frac{y}{z}} %2B \frac{1}{3} \sqrt[3]{\frac{z}{x}} %2B \frac{1}{3} \sqrt[3]{\frac{z}{x}} %2B \frac{1}{3} \sqrt[3]{\frac{z}{x}} }{6}](/2012-wikipedia_en_all_nopic_01_2012/I/9dcfcb83747cdac22adf419f998d6e94.png)
![\ge 6 \cdot \sqrt[6]{ \frac{x}{y} \cdot \frac{1}{2} \sqrt{\frac{y}{z}} \cdot \frac{1}{2} \sqrt{\frac{y}{z}} \cdot \frac{1}{3} \sqrt[3]{\frac{z}{x}} \cdot \frac{1}{3} \sqrt[3]{\frac{z}{x}} \cdot \frac{1}{3} \sqrt[3]{\frac{z}{x}} }](/2012-wikipedia_en_all_nopic_01_2012/I/6fccb8999228ab85992e447d731332a8.png)
![= 6 \cdot \sqrt[6]{ \frac{1}{2 \cdot 2 \cdot 3 \cdot 3 \cdot 3} \frac{x}{y} \frac{y}{z} \frac{z}{x} }](/2012-wikipedia_en_all_nopic_01_2012/I/1a81489fe124459677e06fc1f69afb5d.png)
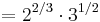
![f(x,y,z) = 2^{2/3} \cdot 3^{1/2} \quad \mbox{when} \quad \frac{x}{y} = \frac{1}{2} \sqrt{\frac{y}{z}} = \frac{1}{3} \sqrt[3]{\frac{z}{x}}.](/2012-wikipedia_en_all_nopic_01_2012/I/11948796a1a2208c21ba3d0a06b3186e.png)
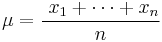
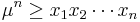
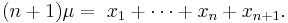
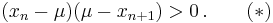
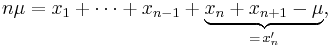
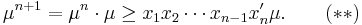
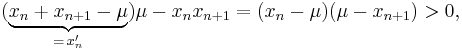


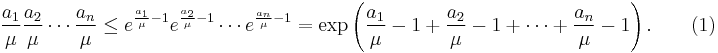
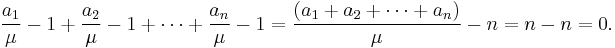
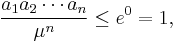
![a_1 a_2 \cdots a_n \le \mu^n \implies \sqrt[n]{a_1 a_2 \cdots a_n} \le \mu.](/2012-wikipedia_en_all_nopic_01_2012/I/bf35b9d6c2bc10eaa63e9c52b9bd767c.png)
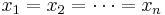
![\begin{align}
x_1 & \ne x_2 \\[3pt]
x_1 - x_2 & \ne 0 \\[3pt]
\left( x_1 - x_2 \right) ^2 & > 0 \\[3pt]
x_1^2 - 2 x_1 x_2 %2B x_2^2 & > 0 \\[3pt]
x_1^2 %2B 2 x_1 x_2 %2B x_2^2 & > 4 x_1 x_2 \\[3pt]
\left( x_1 %2B x_2 \right) ^2& > 4 x_1 x_2 \\[3pt]
\Bigl( \frac{x_1 %2B x_2}{2} \Bigr)^2 & > x_1 x_2 \\[3pt]
\frac{x_1 %2B x_2}{2} & > \sqrt{x_1 x_2}
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/4cf36911301e4ae4ed164b8e101e66b1.png)
![\begin{align}
\frac{x_1 %2B x_2 %2B \cdots %2B x_{2^k}}{2^k} & {} =\frac{\frac{x_1 %2B x_2 %2B \cdots %2B x_{2^{k-1}}}{2^{k-1}} %2B \frac{x_{2^{k-1} %2B 1} %2B x_{2^{k-1} %2B 2} %2B \cdots %2B x_{2^k}}{2^{k-1}}}{2} \\[7pt]
& \ge \frac{\sqrt[2^{k-1}]{x_1 x_2 \cdots x_{2^{k-1}}} %2B \sqrt[2^{k-1}]{x_{2^{k-1} %2B 1} x_{2^{k-1} %2B 2} \cdots x_{2^k}}}{2} \\[7pt]
& \ge \sqrt{\sqrt[2^{k-1}]{x_1 x_2 \cdots x_{2^{k-1}}} \sqrt[2^{k-1}]{x_{2^{k-1} %2B 1} x_{2^{k-1} %2B 2} \cdots x_{2^k}}} \\[7pt]
& = \sqrt[2^k]{x_1 x_2 \cdots x_{2^k}}
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/5078f797a4ea4cca823aa39d62d86b2e.png)
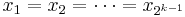
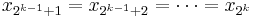
![\frac{x_1 %2B x_2 %2B \cdots %2B x_{2^k}}{2^k} > \sqrt[2^k]{x_1 x_2 \cdots x_{2^k}}](/2012-wikipedia_en_all_nopic_01_2012/I/5be511a9650db2e6ef025a7493d1d91d.png)
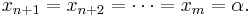
![\begin{align}
\alpha & = \frac{x_1 %2B x_2 %2B \cdots %2B x_n}{n} \\[6pt]
& = \frac{\frac{m}{n} \left( x_1 %2B x_2 %2B \cdots %2B x_n \right)}{m} \\[6pt]
& = \frac{x_1 %2B x_2 %2B \cdots %2B x_n %2B \frac{m-n}{n} \left( x_1 %2B x_2 %2B \cdots %2B x_n \right)}{m} \\[6pt]
& = \frac{x_1 %2B x_2 %2B \cdots %2B x_n %2B \left( m-n \right) \alpha}{m} \\[6pt]
& = \frac{x_1 %2B x_2 %2B \cdots %2B x_n %2B x_{n%2B1} %2B \cdots %2B x_m}{m} \\[6pt]
& > \sqrt[m]{x_1 x_2 \cdots x_n x_{n%2B1} \cdots x_m} \\[6pt]
& = \sqrt[m]{x_1 x_2 \cdots x_n \alpha^{m-n}}\,,
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/bc2e5e9141d6a002a95c74952b8f14ef.png)
![\begin{align}
\alpha^m & > x_1 x_2 \cdots x_n \alpha^{m-n} \\[5pt]
\alpha^n & > x_1 x_2 \cdots x_n \\[5pt]
\alpha & > \sqrt[n]{x_1 x_2 \cdots x_n}
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/10ac985e1d4f8088bd50527bb6471adf.png)
![\ln\biggl(\frac{\alpha_1x_1%2B\cdots%2B\alpha_nx_n}\alpha\biggr)
>\frac{\alpha_1}\alpha\ln x_1%2B\cdots%2B\frac{\alpha_n}\alpha\ln x_n
=\ln \sqrt[\alpha]{x_1^{\alpha_1} x_2^{\alpha_2} \cdots x_n^{\alpha_n}}.](/2012-wikipedia_en_all_nopic_01_2012/I/a6be57150e9570ffa53c12d446a498cd.png)
![\frac{\alpha_1x_1%2B\cdots%2B\alpha_nx_n}\alpha
>\sqrt[\alpha]{x_1^{\alpha_1} x_2^{\alpha_2} \cdots x_n^{\alpha_n}}.](/2012-wikipedia_en_all_nopic_01_2012/I/2c7a90bb14969308b598705e3305d580.png)